 ps
psInteractive graphics is a growing application domain where the demands of latency, bandwidth, and software engineering collide. The state of the art, represented by systems such as QuickDraw GX(R) [QD], Photoshop(tm) [Photoshop], RenderMan(tm) [RenderMan], Explorer(R) [Explorer], and DOOM(tm) [DOOM], is to write in C and assembly language. Programmers use hand-specialized routines, buffering, collection-oriented languages [collection-oriented-languages], and embedded/dynamic languages, but inevitably we face trade-offs in
Run-time code generation (RTCG), as exemplified by Common LISP [CLtL], Pike's Blit terminal [Blit], Masselin's Synthesis operating system [Synthesis], researchers at the University of Washington [KeEgHe91], and elsewhere [DCG][Fabius] is one way to attack this problem. With these systems, one writes programs that create programs. Generating rare cases and fused, one-pass loops as needed directly addresses the program size and latency trace-offs outlined above.
However, RTCG has suffered from a lack of portable, easy-to-use
interfaces. Lisp's quasi-quote, Scheme's syntax-rules [R4RS], and parser generators such as YACC [yacc] automate the
mechanics of constructing certain classes of programs, but it remains
unclear how we can build an RTCG system that is effective on a
wide-range of problems, and is automatic enough that design time and
programmer effort can really be reduced.
Partial evaluation (PE) as described in [JoGoSe93] is a semantics-based program transformation. With the cogen approach the programmer can type-check and debug a one-stage interpreter, then by annotation and tweeking, produce an efficient two-stage procedure (a compiler). Binding times manage program division, memoization handles circularities, and the specializer creates variable names and the rest of the mechanics of code construction. The programmer concentrates on higher-level issues such as staging and generalization. Other current attempts to apply PE to RTCG are Fabius [Fabius] and Tempo [tempo].
This paper explores the application of a directly implemented compiler generator for an intermediate language to pixel-level graphics kernels. The nature of graphics loops is exploited with cyclic integers, which make the remainder (eg modulo 32) of an integer static. A conservative static-equality-of-dynamic-values operator allows static elimination of software caches, thus reducing memory references. The combination of these features allows us to convert bit-level code to word-level code.
For example, say one were converting a packed 24-bit RGB image to
8-bit grayscale. An efficient implementation reads three whole words,
breaks them into twelve samples with static shifts and masks, computes
the four output bytes, and assembles and writes an output word (see
Figure 1) Such a block can make good use of instruction level
parallelism. Our objective is to produce residual code like this from a
general routine (called say image-op) that can handle any channel
organization, bits per pixel, per-pixel procedure, etc.
 ps
psFigure: efficient pixel access
The rest of this paper consists of a system overview followed by a
description of cogen, two examples, and experimental results.
Sections 6 and 7 place the system in context and conclude. Readers not
interested in the intermediate language and its effect on cogen might
read only Sections 2, 4.1, and 4.2.2 before skipping to the examples
in Section 5.
More discussion but few details can be found in [Draves95]. This paper assumes the reader is familiar with binding times, C compilers, LISP macros, caches, and pixels. [FFvDH] provides a good introduction to graphics and [chip-architecture-intro] to chip architecture.
Our system is called Nitrous; within it, we identify three kinds of program transformers (see Figure 1):
root programs from programs in user-defined languages.
cogen for an untyped intermediate language root.
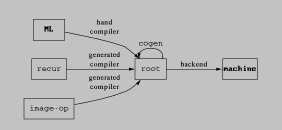 ps
psFigure: System Diagram
root is a simple abstract machine code, like quad-code [Dragon]
with an unlimited number of registers but in continuation-passing
closure-passing style (CPS-CPS) [Appel]. Thus the stack and
closures are explicit data structures and all values are named
uniformly. The model includes reflection and reification [FriedmanWand84], simple data structures, arithmetic, an open set of
primitive functions, and represents higher-order values with closures.
recur is a sample front end. It is a simple recursive equations
language with parallel let, if, and multi-argument procedures.
The cogen-created compiler produces straightforward code. It
compiles tail-recursive calls without building stack frames, but is
otherwise non-optimizing.
Image-op is the hypothetical procedure described above. The
compiler might be run when the user opens a new file, repositions a
window on the screen, chooses a new brush, etc.
A compiler generator transforms an interpreter into a compiler. That
is, cogen transforms a root program and binding times (BTs)
for its arguments into a generating extension. The BTs
categorize each argument as static program or dynamic data;
essentially they are types [Henglein91]. The extension
consists of a memo table, followed by the static parts of the
computation interleaved with instructions that generate residual code
(ie do RTCG).
The backend executes root programs. We examine current and future
backends in Section 5.3.
By supporting reflection we make code-producing functions first class.
Nitrous takes this a step further by making the compiler-producing
function (cogen) first class: rather than working with files, it
just maps procedures to procedures. To facilitate this the backend
supports reification: the root text of any code pointer can be
recovered.
Because the compilers produce the same language that cogen accepts,
and the root text of the residual programs is easily accessible,
multiple layers of interpretation can be removed by multiply applying
cogen. The lift compiler (see Section 4.2) works this way; other
possibilities include using recur to create input for cogen, or
providing a compiler generator as a primitive in the recur language.
Such multi-stage application requires that the generated compilers
create correctly annotated programs, which can be difficult. In [GluJo94] and [GluJo95] Glück and Jørgensen
present more rigourous and automatic treatments of layered systems
using specializer projections and multi-stage binding-time analysis.
The core of the system is the intermediate language root. Its
formal syntax appears in Figure 3. A program is called a code
pointer, or just a code. When a code is invoked, its formal
parameter list is bound to the actual arguments. The list of prim
and const instructions execute sequentially, each binding a new
variable. if tests a variable and follows one of two instruction
streams. Streams always terminate with a jump instruction, which
transfers control to the code bound to the first argument and passes
the rest. Formal semantics can be found in [Draves95].
code ::= (code name args instrs)
instr ::= (prim v prim . args)
| (const v constant)
| (if v true-branch)
| (jump v . args) |
v ::= variable instrs ::= instr list args ::= variable list true-branch ::= instrs prim ::= primitive operation |
Figure: root syntax
Structured higher-order control flow is managed with closure-passing [Appel]. A closure pairs a code pointer with its bound variables, and is invoked by jumping to its car and passing itself as the first argument. Normal procedure call passes the stack as the next argument. The stack is just the continuation, which is represented with a closure. See Figure 4 for an example.
append(k l m) {
if (null? l) (car k)(k m) a
frame = (list k l m)
cl = (close cont frame) b
append(cl (cdr l) m)
} |
cont(self r) {
(k l m) = (cdr self) c
nr = (cons (car l) r)
(car k)(k nr)
} |
Figure:
root code for append, in sugary-syntax. Notes: a return
by jumping to the car of k, passing k and m as arguments.
b close is like cons, but identifies a closure. c
destructuring assignment.
Factors that weight in favor of an intermediate language like root
include: root 1) makes cogen smaller and easier to write; 2)
provides target for a range of source languages; 3) provides an
interface for portability; 4) opens opportunity to schedule large
blocks and utilize instruction level parallelism; 5) exposes language
mechanism (such as complex optional arguments and method lookup) to
partial evaluation; 6) reduces assembly overhead because it is
essentially an abstract RISC code; 7) allows expressing optimizations
not possible in a High Level Language.
And against: 1) types would simplify the implementation and formalization; 2) good loops (eg PC-relative addressing) are difficult to produce; 3) explicit stacks and exceptions would reduce consistency requirements and make optimization easier; 4) using a language like GCC [GCC], OmniVM [OmniVM], or the G-machine [implementation-functional-languages] would leverage existing research.
cogen is directly implemented (rather than produced by
self-application), polyvariant (allows multiple binding time patterns
per source procedure), handles higher-order control flow, and is based
on abstract interpretation. This section summarizes how cogen and
its extensions work, in theory and practice. The subsections cover
binding times, cyclic integers, lifting, termination, and special
primitive functions in greater detail.
cogen converts a code and a binding-time pattern to an extension.
An extension is identified with the name of the code pointer and the
BT pattern, for example append(.
D S D)
The extensions memoize on static values to produce programs with loops. Arbitrary dynamic control flow can be produced: a recursive equations language can specify any graph. The interaction between cyclic arithmetic and memoization can result in a least common multiple (LCM) computation.
To support variable splitting and inlining the extension renames the variables in the residual code and keeps track of the shapes (names and cons structure) of the dynamic values. The shape of a dynamic value is the name of its location. Shapes are part of the key in the static memo table; two shapes match if they have the same aliasing pattern, that is, not only do the structures have to be the same, but the sharing between parts of the structures must be the same. The effect of variable splitting is that the members of a structure can be kept in several registers, instead of allocated on the heap (abstracted into one register).
Inlining is controlled by the dynamic conditional heuristic [Similix], but setting the special $inline variable overrides the
heuristic at the next jump.
In CPS-CPS continuations appear as arguments, so static contexts are
naturally propagated. Figure 5 shows the translation of (+ into S (if
D 2 3))root. The extension dyn-if(D S D) calls the
extension cont((.
![]() S (
S (![]() D S D)) D)
D S D)) D)
dyn-if(k s d) {
frame = (list k s d)
cl = (close cont frame)
if (d) (car cl)(cl 2)
(car cl)(cl 3)
} |
cont(self r) {
(k s d) = (cdr self)
rr = r + s
(car k)(rr)
} |
Figure: Propagating a static context past a dynamic conditional.
Binding times are the metastatic values from self-applicable PE. They represent properties derived from the interpreter text while a compiler generator runs. Primarily they indicate if a value will be known at compile time or at run-time, but they are often combined with the results of type inference, control flow analysis, or other static analyses.
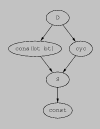 ps
psFigure: Lattice Order. (![]() c)<
c)<S<cyc<D
cogen's binding-time lattice appears in Figure 6. Cons cells are
handled with graph grammars as in Mogensen [Mogensen89]: pairs in
binding times are labeled with a `cons point'. If the same label
appears on a pair and a descendant of that pair then the graph is
collapsed, perhaps forming a circularity. An annotation may provide
the label, much like a type declaration.
We denote a pair ( (the label is
invisible here). ![]() bt bt)
bt bt)( abbreviates ![]() x y ...)
x y ...)(. In the
lattice, ![]() x (
x (![]() y ... (
y ... (![]() nil)))
nil)))S<(![]() bt bt)<
bt bt)<D
For example, a value with BT D list has no static value, but its
shape is a list of variable names. The dynamic values are placed in
registers as space permits.
As in Schism [Consel90], control flow information appears in the
binding times. cogen supports arbitrary values in the binding
times, including code pointers, the empty list, and other type tags.
Such a BT is denoted (, or just c.
![]() c)
c)
Closures are differentiated from ordinary pairs in the root text,
and this distinction is maintained in the binding times. Such a
binding time is denoted (.
![]() bt bt)
bt bt)
An additional bit on pair binding times supports a sum-type with atoms. It is not denoted or discussed further.
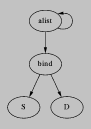 ps
ps  ps
ps 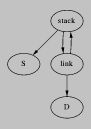 ps
psFigure: Three binding times: (S * D) list is an association list
from static keys to dynamic values, D list is a list only whose
length is static, stack-bt is the binding time of a control
stack.
There are many ways of dividing integers. Nitrous can break an
integer into static base, dynamic quotient, and static
remainder[footnote: Here's another way to divide integers: a static
bitmask divides the bits into static and dynamic.]: ![]() . Such a
binding time is denoted
. Such a
binding time is denoted cyc. If ![]() is a power of two (eg 32)
then we have a static bit field (eg the 5 low bits are static). In
the lattice,
is a power of two (eg 32)
then we have a static bit field (eg the 5 low bits are static). In
the lattice, S<cyc<D.
We have to make special cases of all the primitives that handle cyclic values. The easiest are addition and multiplication. The static code works like this:
v = (+ s (cyclic b q r)) --> v = (cyclic b q (+ s r)) v = (* s (cyclic b q r)) --> v = (cyclic (* s b) q (* s r)) v = (+ s d) --> v = (cyclic 1 d s) v = (* s d) --> v = (cyclic s d 0)On the left is a source instruction with binding times, on the right is the code in the extension. No case has any dynamic component; because the quotient passes through unchanged we can just copy the shape (
q). Rules for (+ cyc cyc) and (* cyc cyc) might
also be useful, but are not explored in this paper.
zero?, imod, and idiv are more compicated because the
binding time of the result depends on the static value. For zero?,
if the remainder is non-zero, then we can statically conclude that the
original value is non-zero. But if the remainder is zero, then we
need a dynamic test of the quotient. This is a conjunction
short-circuiting across binding times. It makes direct use of
polyvariance.
v = (zero? (cyclic b q r)) --> if (zero? (imod r b))
emit v = (zero? q)
v = #f
See Section 4.2.2 for a brief description of the other affected primitives.
Note that the rule given for addition doesn't constrain the remainder
to 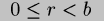 by overflowing into the quotient as one would
expect. Instead, the congruence modulo
by overflowing into the quotient as one would
expect. Instead, the congruence modulo ![]() is maintained only at
memo points: this is late normalization of cyclic values. The
extra information propagated by this technique (early-equality across
cycles) is required to handle multiple overlapping streams of data.
is maintained only at
memo points: this is late normalization of cyclic values. The
extra information propagated by this technique (early-equality across
cycles) is required to handle multiple overlapping streams of data.
Thus when the compiler begins to make a dynamic code block, all cyclic
values are normalized by adjusting r to satisfy 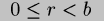 .
This is done by emitting counter-acting additions to q. The
sharing between these values must be maintained across this
adjustment.
.
This is done by emitting counter-acting additions to q. The
sharing between these values must be maintained across this
adjustment.
Lifting is generalization, or `abstracting away' information. If we abstract away the right information the compiler will find a match in its memo table, thus proving an inductive theorem. The simplest lift converts a known value to an unknown value in a known location (virtual machine register). Lifting occurs when
code is converted to a static value. It is replaced
with its extension, this requires a binding time.
prim has arguments of mixed binding time, causing all the
arguments to be lifted.
jump has dynamic target, causing all the arguments to be
lifted.
Lifting is inductively defined on the binding times. The base cases are:
S --> D allocates a dynamic location and initializes it to
the static value.
cyc --> D emits a multiplication by the base
(unless it is one) and addition with the remainder (unless it is
zero).
S --> cyc results from an annotation used to
introduce a cyclic value. The conversion is underconstrained;
currently a base of one is assumed.
(
D D) --> D emits a dynamic cons
instruction.
( (
(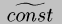 p) frame)
p) frame) --> D generates and inserts a call to p((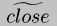
D x) D D ...) (all but the first argument are D), then emits
the cons.
(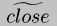 S frame)
S frame) --> D same as
the previous case, but the extension has already been computed, so just
emits a call and a cons.
Case 5 is particularly interesting. Any static information in frame is saved by reassociating it into the code pointer before it is lifted. This introduces a complication, as explained in Section 4.3 below. The lift compiler handles applying these cases to structured and circular binding times.
Manual lifting is supported in root with an instruction understood
by cogen but ignored by the root semantics:
instruction ::= ... | (lift v) | (lift v bt) | (lift v (args) proc)
The variable v is lifted to D, unless the target bt is
given. Any legal lift is supported, including lifting to/from
partially static structures with loops and closures. Instead of
giving a binding time bt, one can give a procedure proc
which is executed on the binding times of args. This provides a
rudimentary lift language.
If a lift isn't one of the base cases outlined above, then the lift compiler is invoked to create a procedure that takes the value
apart, applies simple lifts at the leaves, and reassembles the
structure. cogen inserts a call to this procedure into the source
program, and recurses into it.
For example, consider the lift (S * D) list-->D. The
compiler has a list of values and a list of variable names. It
recurses down the lists, and emits a const and a cons instruction
(making a binding) for each list member. At the base it recovers the
terminator, then it returns up and emits cons instructions that build
the spine.
It turns out that this lift compiler can be created by cogen itself.
The meta-interpreter is just a structure-copy procedure that traverses
the value and the binding times in parallel. A delayed lift
annotation is used where the BTs indicate a simple lift. Specializing
this to the binding times results in a copy function with lifts at the
leaves. The value passed to the copy function has the binding
time that was just a static value. When the continuation is finally
called the remaining static information is propagated. The copy
function may contain calls to itself (where the BT was circular) or to
other extensions (to handle higher-order values).
This is an example of multi-stage compiler generation because the
output of a generated compiler is being fed into cogen. The
implementation requires care as cogen is being used to implement
itself, but the possibility of the technique is encouraging.
cogen treats some primitive functions specially, generally in order
to preserve partially static information. Figure 8 gives the improved
binding times possible, and in what situations they occur. Notes:
root is untyped.
null? and atom? are also supported.
apply takes two arguments: a primitive (in reality, a
C function) and a list of arguments. If the primitive and the
number of arguments are static, then the compiler can just generate the
primitive instead of building an argument list and generating an apply. This supports interpreters with an open set of primitives
or a foreign function interface. Notice this doesn't improve the
binding times, it just generates better code.
S and D are created, the
compiler chooses one statically (see Section 4.1.1).
v = (imod (cyclic b q r) s) --> if (zero? (imod b s))
v = (imod r b)
error
imod but
v = (idiv (cyclic b q r) s) --> if (zero? (imod b s))
v = (cyclic (idiv b s) q r)
error
Note that it is necessary that the division primitive round down even
for negative inputs, ie (idiv -1 10) --> -10.
early= conservative static equality of dynamic values, see
Section 5.1.
(identity x) x a (cons S S) Sb (cons S D) (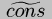
S D) (cons D D) (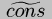
D D) c (car (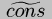 x y))
x y)) x (pair? (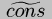 _ _))
_ _)) Sd (apply S (D list)) De
(+ cyc S) cyc(* cyc S) cyc(+ D S) cyc(* D S) cyc(zero? cyc) both f (imod cyc S) Sg (idiv cyc S) cych (early= D D) Si
Figure: See the text for notes.
Because the stack is an explicit argument, when cogen encounters a
static recursion the same label will eventually appear on two stack
frames. In theory, because (, when this loop is collapsed the metastatic continuations
would be lifted to static, thereby converted to extensions and forming
a control stack in the compiler. However, to simplify the
implementation ![]() x)
x) ![]() (
(![]() y) =
y) = Scogen uses a special lift that supplies the return
BT(s) and sets up the stack:
instruction ::= ... | (lift v stack ret-bt ...)
This causes the lift ( and uses extension ![]() p frame) --> stack-bt
p frame) --> stack-btp(( to create the extension for the continuation.
![]()
S frame)
ret-bt ...)
For example, consider append([footnote: Only a more
complex recursion really requires this, but D S D)append is easier to
understand.], with lift directives as it shown in Figure 8. The key
sequence of extensions and lifts that create the recursion appears in
Figure 9. cogen could avoid producing the (probably over-)
specialized entry/exit code by checking for the end of the stack
explicitly.
append(k l m) {
if (null? l) (car k)(k m)
frame = (list k l m)
cl = (close cont frame)
lift cl stack dynamic
append(cl (cdr l) m)
} |
cont(self r) {
(k l m) = (cdr self)
nr = (cons (car l) r)
lift nr
(car k)(k nr)
} |
Figure: Annotated code for a static recursion.
append( |
append(stack-bt |
Figure: Building a static recursion.
Here we consider lift case 5 from Section 4.2 in greater detail. Say
f has one argument besides itself. Then lifting ( creates a call to the extension ![]() f
frame) -->
f
frame) --> Df((. The extension is used to fold the
static part of frame into ![]()
D frame) D)f. The problem is, according to
its binding-time pattern, the extension expects the dynamic part of
the frame to be passed in separate registers (because of variable
splitting), but at the call site the value is pure dynamic, so they
are all stored in one register.
Nitrous uses special code at the call site to save (lift) the shape, and in the extension wrapper to restore (unlift) the shape. This code optimizes the transfer by only saving each register once, even if it appears several times in the shape (typically a lexical environment appears many times, but we only need to save the subject-values once). The same optimization prevents a normal jump from passing the same register more than once.
How do we extract the dynamic stack of a recur program from the
stack in the recur interpreter? Say cogen encounters do-call(stack-bt (see Figure 10). When
S S alist-bt)cl is lifted we compute cont((. We want to generate a procedure call where ![]()
S (![]() stack-bt
stack-bt S)) D)cont jumps to apply, so inlining is disabled and we lift the
stack (k) to D, invoking lift base case 4. The problem is the
extension was made assuming the code pointer would be static, but now
it will be dynamic. The unlift code inserts an additional cdr to skip
the dynamic value, thus allowing an irregular stack pattern to be
handled.
do-call(k fn exp env) {
frame = (list k fn)
cl = (close cont frame)
lift cl stack dynamic
eval(cl exp env) a
} |
cont(self arg) {
(k fn) = (cdr self)
lift k
$inline = #f
apply(k fn arg)
} |
Figure: annotated code to produce a dynamic stack frame. Notes: a the call to evaluate the argument is inlined.
Alternative Representations of Cyclic Values
Cyclic values as described in Section 4.1 are inadaquate for the filter example described below. The problem is the addresses are cyclic values so before you can load a word the address must be lifted, resulting in a dynamic multiplication and addition. The way to solve this is to use a different representation: rather than use q as the dynamic value, one can use bq. This is premultiplication. On most RISC architectures the remaining addition can be folded into the load instruction.
The disadvantage of premultiplication is that multiplication and division can no longer maintain sharing information. Which representation is best depends on how the value is used. A simple constraint system should suffice to pick the correct representation.
This section presents examples of the code transformations possible with Nitrous, and measures their effect on time consumed. Two graphics examples are examined in the subsections, then the benchmark data is presented.
These examples make novel use of partial evaluation to optimize memory
access by statically evaluating alignment and cache computations.
Thus code written using a load-nybble procedure (with bit
pointers) can be converted to code that uses load-word and static
shifts and masks.
Say we sequentially access the elements of a vector of packed sub-word-sized nybbles[footnote: Historically `nybble' means precisely four bits. I have adopted the term to mean anything from one to thirty-one bits.]. Figure 12 gives code for reducing a vector of nybbles. The code on the right is specialized to 8 bits per nybble and a bit vector length to zero mod 32. There are three things going on:
zero? tests are done in
the compiler before it reaches an even word boundary and emits a
dynamic test. These adjacent iterations of the loop can run in
parallel.
(imod cyc S) is static.
Shifts with constant offsets generally take one fewer register of
space and one fewer cycle in time.
load-word_c instead of the load-word
primitive.
The hard part is making the cache work: the cache-present test has
dynamic arguments, but it must be eliminated. This is exactly the
purpose of early=, it returns true if the compiler can prove the
values are equal (are aliases). Since the shapes track the locations
of the dynamic values, this is accomplished just by testing them for
equality. Note how this equality information is propagated through
the idiv primitive.
Note that in the actual implementation, a store is threaded through the code to provide the state for the memory and its cache.
Even if the index were completely dynamic we could still use this fast loop by applying the Trick to make it cyclic.
i = cyclic; sum = D
while (i) {
i = i - bpn
nyb = load-nybble(i bpn)
sum += nyb
}
|
while (iq) {
iq = iq - 1
w = load_word(iq)
sum += (w >> 24) & 255
sum += (w >> 16) & 255
sum += (w >> 8) & 255
sum += (w >> 0) & 255
}
|
Figure: General and specialized code to reduce a vector of nybbles. For simplicty, this code doesn't handle nybbles that overlap words.
load-word_c(cache)(addr) {
if (early= addr cache.addr)
w = cache.word
w = (load-word addr)
cache = (list addr w)
return w
}
|
w2n(w bpn ny) {
mask = ((1 << bpn) - 1)
r = mask & (w >> (ny * bpn))
return r
}
|
Figure: Helper functions.
1D Filtering with Software Cache
A one-dimensional finite-response filter transforms an input stream of samples into an output stream by taking a sliding dot-product with a constant kernel-vector (see Figure 14). If the kernel has length k then each word is loaded k times. If one makes the outer loop index be cyclic base k, then in the residual code the loop is expanded and the loads are shared. A window on memory is kept in registers but rather than rotating it, we rotate the code around it.
As before, this can be done using a caching load procedure, though the
cache now must maintain several values. A cache has BT (cyc * S *
D) list, the tuple is of the address, the dirty bit (or other cache
control information), and the word from memory. The length of the
list controls the cache's size, this must be set manually. The cache
is managed with the Least Recently Used (LRU) policy. The entry code
that `fills the pipeline' is produced automatically because the
memo-test doesn't hit until the cache gets warm.
This example was the motivation for the late normalization described
above. The address p is kept premultiplied to avoid a
dynamic multiplication when it is lifted at every load.
stride = S; kernel = S
p = cyc; q = D; klen = S
while (p) {
dp = dot(0 p kernel klen)
store_word(q dp)
p -= stride
q--
}
|
w0 = load-word(p)
w1 = load-word(p-1)
w2 = load-word(p-2)
sum = 2*w0+5*w1+2*w2
store-word(q sum)
p -= 3; q++
while (p-=3) {
w0 = load-word(p)
sum = 2*w1+5*w2+2*w0
store-word(q sum)
w1 = load-word(p-1)
sum = 2*w2+5*w0+2*w1
store-word(q+1 sum)
w2 = load-word(p-2)
sum = 2*w0+5*w1+2*w2
store-word(q+2, sum)
q += 3;
}
|
Figure: General and specialized finite filter code. The kernel is [2 5 2] and the stride is one.
Implementation, Backend, and Benchmarks
cogen is written in Scheme48 [Scheme48], which compiles an
extended Scheme to bytecode[footnote: In fact the bytecode interpreter
is written in Pre-Scheme [pre-scheme] and compiled to C.].
cogen is 2000 lines, supported by 4000 lines of utilities, the
virutal root backend, the compiler to GCC, examples, test cases,
etc. It has not yet been optimized for speed (eg it doesn't use
hashing or union-find). The source code and transcripts of sample
runs are available from http://www.cs.cmu.edu/~spot/nitrous.html.
Except for the lift compiler (see Section 4.2) the only working front
end is a macro assembler, using Scheme as the macro language. So far
the code fed to cogen has been written in root (with lift
annotations) by hand. The recur compiler produces good code but is
unfit for use as a front end because it does not yet produce
annotated code.
The hypothetical ideal backend performs register allocation, instruction selection and scheduling, dead-code elimination, constant sharing, and linking to convert this language into executable code. I am budgeting about 2000 instructions to produce each dynamic instruction.
The backend used to produce these benchmarks translates a whole root
program to a single GCC [GCC] function which is compiled, run,
and timed using ordinary Unix(tm) tools. The run-time is just 350
lines of C and does not support garbage collection. These times are
on a 486DX4/75 running linux (x86), and a 150Mhz R4400 SGI Indy
(mips).
Support for reification and reflection is trivial in the interpreted virtual machine, but non-existent in the GCC backend. The ideal backend would support reflection either by transparent lazy compilation or with a `compiling eval' procedure in the run-time. Reification could be supported by keeping a backpointer to the intermediate code inside each code segment (unless proven unnecessary).
The benchmark programs are summarized below:
recuratree performs a mixture of arithmetic and procedure
calls, even tests the parity of 100 by mutual recursion, append a list of length 5 in the usual way.
In the nybble and filter examples, the nitrous-int code uses calls to the cached memory operations, but the cache size is set to zero. The manual-int code uses ordinary loads.
The numbers are reported in Figure 15. Appreciable speed-ups are
achieved in most cases. The hand-written C code is about twice as
fast as the compiled root programs. We speculate that this is
because we use `computed goto' and the && operator for all control
flow.
| mips | x86 | |||||||
| nitrous | manual | nitrous | manual | |||||
| int | spec | int | spec | int | spec | int | spec | |
| recur atree | 100 | 2.5 | 600 | 15 | ||||
| recur even | 1900 | 3.7 | 11000 | 13 | ||||
| recur append | 150 | 3.6 | 710 | 23 | ||||
| nybble 4 | 12000 | 160 | 380 | 140 | 64000 | 460 | 1500 | 380 |
| nybble 12 | 4700 | 77 | 180 | 59 | 25000 | 210 | 680 | 170 |
| filter 3 | 6500 | 140 | 400 | 45 | 53000 | 620 | 650 | 230 |
| filter 7 | 13000 | 380 | 880 | 68 | 110000 | 760 | 1400 | 450 |
Figure:
Benchmark data, times in microseconds, two digits of precision. All
time trials run five times; best time taken. The `int' columns are
for the general interpreters; and `spec' for the specialized residual
code. The `nitrous' columns are for code written in root and
produced by cogen, and `manual' for normal C code written by hand.
Related Work and Alternate Paths
This section places Nitrous in context of computer graphics systems practice, and other research in partial evaluation and RTCG. First, we list the standard approaches to the generality/performance trade-off with a collection of examples of each.
Hardware support for byte-pointers and an on-chip cache have similar effect as our loop optimizations (the hardware repeats the computation, but the hardware is very fast). However, note that the Alpha [Alpha] doesn't support byte pointers, and DSP chips sometimes provide an addressing mode for on-chip SRAM bank, rather than a cache. This is an application of RISC philosophy (factoring from hardware into the compiler to increase the clock rate).
Similix [Similix] is a sophisticated, freely-available compiler generator. It uses a type-inference BTA, supports higher order Scheme-like language with datatypes and an open set of prims. It supports partially static structs, simple manual lifts, and is monovariant. It produces small programs and runs fairly quickly. It's file-based interface could be combined with a Scheme compiler (provided it had the right interface) to do RTCG. Schism [Schism] is similar but nicer.
DCG [DCG] and [KeEgHe93] provide C-callable libraries for RTCG. They use typical C-compiler intermediate language for portable construction and fast compilation with `rudimentary optimization'. The ratio of static instructions used per dynamic instruction produced is 300 to 1000.
`C [tick-C] augments C with backquote-like syntax to support manual RTCG. It provides a nice interface to DCG, and can handle complex interpreters (eg Tiny-C). By retargetting C-mix [cmix] to `C one might be able to combine the strengths of these systems (constraint-based BTA, fast code generation, a popular language).
Fabius [Fabius] is a compiler generator for a simplified first-order ML-like language. The programmer uses curry notation to specify the program division, and a BTA completes it. This is a very natural means of annotation. The compilers produce machine code directly, thus they are very fast; its ratio is about 7.
Tempo [tempo] is a off-line, template-based specializer for C aimed at operating systems code. It contains sophisticated pointer analyses and other features to make it work on `real' systems. So far no results are available.
Staging transformations [JoSche86], ordered rewriting [DeRe93], program slicing [Slicing], and metaobject protocols [Kiczales92] contain related ideas from other parts of the language research community.
Conclusion and Future Directions
We have described Nitrous, a run-time code generation system for interactive graphics. It uses compiler generation of intermediate code to provide sophisticated transformations with low overhead. It augments standard partial evaluation techniques with new annotations and binding times. While the preliminary results from the graphics kernels are promising, the front and backend are still too incomplete to conclusively demonstrate the utility of this approach. Besides the immediate goals of fleshing out the system and scaling up the experiments, we hope to
This paper was partially written and researched while visiting DIKU and DAIMI with funding from the Danish Research Council's DART project. I would like to thank Olivier Danvy, Nick Thompson, and the anonymous reviewers for their comments on drafts of this paper, and Peter Lee for his continuing feedback, faith, and support.