 ps
psMedia such as audio, images, and video are increasingly common in computer systems. Such data are represented by large arrays of small integers known as samples. Rather than wasting bits, samples are packed into memory. Figure combined illustrates three examples: monaural sound stored as an array of 16-bit values, a grayscale image stored as an array of 8-bit values, and 8-bit values compressed with run-length encoding. Figure rgbm3d shows a color image stored as interleaved 8-bit arrays of red, green, and blue samples. Such ordered collections of samples are called signals. A constant signal may avoid memory usage completely.
 ps
ps
We begin by considering only signals that are regular arrays. Say we
specify a signal's representation with four integers: from and to are bit addresses; size and stride are numbers of bits.
The signal itself is stored in memory as a array where the distance
(in bits) between elements is the stride, and the number of bits per
element is the size. I use little-endian addressing so the least
significant bit of each word (LSB) has the least address of the bits
in that word.
type baddress = int
type signal = baddress * baddress * int * int
(* from to size stride *)
Figure sum-signal gives the code to sum the elements of such a
signal. As in Chapter intro, the examples use ML syntax
extended with infix bit operations and a load_word primitive.
This chapter assumes 32-bit words, but any other size could just as
easily be substituted, even at run-time. The integer division (/)
rounds toward minus infinity, and the integer remainder (%) has
positive base and non-negative result. To simplify this presentation,
load_sample does not handle samples that cross word boundaries.
This procedure is the beginning of the bit-level abstraction.
fun sum (from, to, size, stride) r =
if from = to then r else
sum ((from + stride), to, size, stride)
(r + (load_sample from size))
fun load_sample p b =
((1 << b) - 1) &
((load_word (p / 32)) >> (p % 32))
If I fix the layout of the input to sum by assuming that
stride = size = 8 and (from % 32) = (to % 32) =
0
fun sum_0088 from to r =
if from = to then r else
let val v = load_word from
in sum_0088 (from + 1) to
(r + (v & 255) + ((v >> 8) & 255) +
((v >> 16) & 255)+ ((v >> 24) & 255))
end
Different assumptions result in different code. For example,
sequential 12-bit samples result in unrolling 8=lcm(12,32)/12 times so
that three whole words are loaded each iteration (see Figure twelve). Handling samples that cross word boundaries requires adding
a conditional to load_sample that loads an additional word, then
does a shift-mask-shift-or sequence of operations. The actual
implementation appears in Appendix cache.
This chapter shows how to use a specializer to derive code like Figure fast-sum from the code in Figure sum-signal automatically. First I introduce cyclic integers, which provide intelligent unrolling. Next, I show how to implement a cache in software to optimize loads and stores. Finally some limitations of this approach are revealed.
This section shows how adding some rules of modular arithmetic to the
specializer formalized in Chapter pe can unroll loops, make
shift offsets static, and eliminate the division and remainder
operations inside procedures like load_sample.
Figure domains2 defines the ![]() domain, redefines
domain, redefines ![]() to
include
to
include ![]() as a possible meaning, and extends
as a possible meaning, and extends ![]() to handle cyclic
values. Whereas previously an integer value was either static or
dynamic (either known or unknown), a cyclic value has known base and
remainder but unknown quotient. The base must be positive. If the
remainder is non-negative and less than the base, then I say the
cyclic value is in normal form. For now, assume all cyclic
values are in normal form.
to handle cyclic
values. Whereas previously an integer value was either static or
dynamic (either known or unknown), a cyclic value has known base and
remainder but unknown quotient. The base must be positive. If the
remainder is non-negative and less than the base, then I say the
cyclic value is in normal form. For now, assume all cyclic
values are in normal form.
Figure addmult0 gives one way to extend ![]() for cyclic
values. Again I assume cases not given are avoided by lifting,
treating the primitives as unknown (allowing
for cyclic
values. Again I assume cases not given are avoided by lifting,
treating the primitives as unknown (allowing ![]() to match any
primitive), or by using the commutivity of the primitives. A case for
adding two cyclic values by taking the GCD of the bases is
straightforward, but has so far proven unnecessary. Such
multiplication is also possible, though more complicated and less
useful. The static result of multiplication by zero is a standard
online optimization, but is not important to this work.
to match any
primitive), or by using the commutivity of the primitives. A case for
adding two cyclic values by taking the GCD of the bases is
straightforward, but has so far proven unnecessary. Such
multiplication is also possible, though more complicated and less
useful. The static result of multiplication by zero is a standard
online optimization, but is not important to this work.
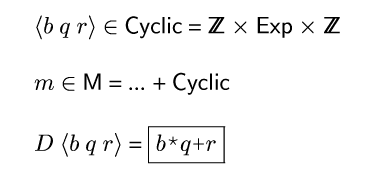

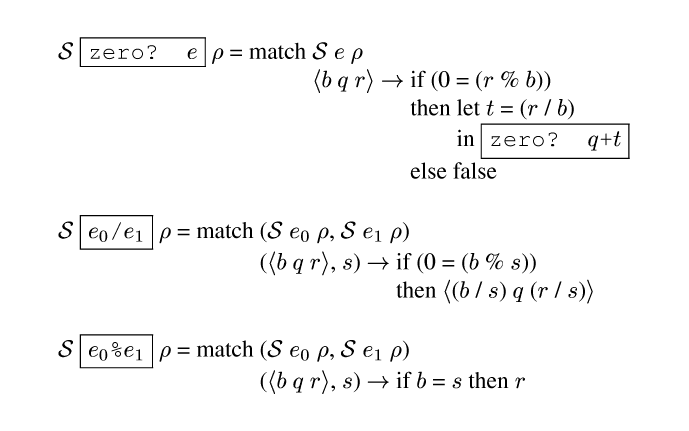
Figure morerules gives rules for zero?, division, and
remainder. In the case of zero?, if the remainder is non-zero
modulo the base, then the specializer can statically conclude that the
original value is non-zero. But if the remainder is zero, then we
need a dynamic test of the quotient. This is a conjunction
short-circuiting across stages.
These rules are interesting because the binding times of the results depend on static values rather than just the binding times of the arguments. The result is an example of what in partial evaluation parlance is called polyvariance in binding times.
The rules for division and remainder could also include cases that returned a dynamic result when the condition on the base is not met. But this would create larger or slower compilers and has not proven to be useful, so my systems just raise an error.
The approach of this chapter has been binding-time improvement by extending the specializer. Instead, one could rewrite the source program to make the separation apparent to an ordinary specializer. This can be done by defining (in the source language) a new type which is just a partially static structure with three members. The rules in Figures addmult0 and morerules become procedures operating on this type. The source program must be written to call these procedures instead of the invoking the native arithmetic (this is done with Similix in Appendix ba).
As it turns out, the rules in Figure addmult0 have several defects. Section npi explains them and a way to overcome them. Note that the solution presented there cannot also be implemented as a manual binding time improvement.
Now I explain the effect of cyclic values on the sum example from
Figure sum-signal. The residual code appears in Figure resid1. Assumption 1 above directly means that from and to
are cyclic. The end-test for the loop compares these values by
calling zero? on the difference. As long as the remainders
differ, the end-test is statically known to be false. Thus three
tests are done in the compiler before it reaches an even word
boundary, emits a dynamic test, and forms the loop. All shifts and
masks are known at code generation time, allowing immediate-mode
instruction selection on common RISC architectures. If one were
compiling to VLSI hardware, this might be particularly useful, as
these operations become almost free with good layout[footnote: VLSI
represents data with voltages in wires on a two-dimensional surface.
With Field Prorammable Gate Arrays (FPGA), the hardware can be
reconfigured in about a millisecond. [SiHoMcA96] reports on
using partial evaluation to dynamically reconfigure FPGA chips.].
These results depend on the style of input. For example the program in Figure badl represents a signal with its start address and length in samples. Since the loop works by counting the samples instead of comparing addresses, no conditionals are eliminated.
![{ml {Spec} {m sum} [{tab-stop}{c from}{mapsto}{angle 32 {frame-box {c fromq}} 0}{space 5mm}{c to}{mapsto}{angle 32 {frame-box {c toq}} 0}
{tab}{c size}{mapsto}8{space 5mm}{c stride}{mapsto}8{space 5mm}{c r}{mapsto}{frame-box {c r}} ]
}](53.gif) -->
-->
fun sum_0088 fromq toq r =
if fromq = toq then r else
sum_0088 (fromq + 1) toq
(r + (((load_word fromq) >> 0) & 255) +
(((load_word fromq) >> 8) & 255) +
(((load_word fromq) >> 16) & 255) +
(((load_word fromq) >> 24) & 255))
fun sum2 (from, length, size, stride) r =
if length = 0 then r else
sum ((from + stride), length-1, size, stride)
(r + (load_sample from size))
sum fails to specialize as
well.
Note that the dynamic part of the cyclic values is represented by the quotient. See Section cyc-rep for more on this.
If the alignments of from and to had differed, then the odd
iterations would have been handled specially before entering the loop.
The generation of this prelude code is a natural and automatic result
of using cyclic values; normally it is generated by hand or by
special-purpose code in a compiler.
If we want to apply this optimization to a dynamic value and we can afford to spend some code-space, then we can use case analysis to convert the dynamic value to cyclic before the loop. This results in one prelude for each possible remainder, followed by a single loop, as explained in Section setbase.
Arbitrary arithmetic with pointers can result in values with any base,
but once we are in a loop like sum we want a particular base. Set-base allows the programmer work around this. Figure sbe
shows an example of its use. Section setbase explains its
implementation.
While we currently rely on manual placement of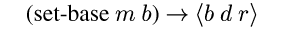
set-base, we
believe automation is possible because the analysis required appears
similar to the un/boxing problem [Leroy92].
fun vector_signal from to stride size =
let val from = set_base from 32
and to = set_base to 32
in
fn s_get => load_sample from size
| s_put => fn v => store_sample from size v
| s_next => vector_signal (from+stride) to stride size
| s_end => from = to
end
set-base. This code is from the higher-order
implementation of the signal interface (Figure sig). It is
the only use of set-base in the implementation.If a loop reads from multiple signals simultaneously, then in order to apply the these optimizations, it must be unrolled until all the signals return to their original alignment. Figure msig illustrates such a situation. The ordinary way of implementing a pair-wise operation on same-length signals uses one conditional in the loop because when one array ends, so does the other. Since our unrolling depends on the conditional, this would result in ignoring the alignments of one of the arrays.
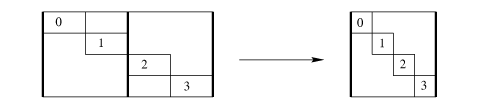 ps
ps
To solve this, we perform such operations with what normally would be
a redundant conjunction of the end-tests. Figure binop
illustrates this kind of loop. In both implementations the residual
loop has only one conditional, though after it exits it makes one
redundant test[footnote: Simple does this because its compiler to C
translates while(E&&F)S to while(E)while(F)S. Nitrous does
this because its input language is in continuation passing style].
Because 32 has only one prime factor (2), on 32-bit machines this amounts to taking the maximum of all of the signals. If the word-size were composite then more complex cases could occur. For example, a 24-bit machine with signals of stride 8 and 12 results in unrolling 6 times, as illustrated in Figure b24.
fun redbin (from0, to0, size0, stride0)
(from1, to1, size1, stride1) =
if ((from0 = to0) andalso (from1 = to1))
then ()
else (... ; redbin( ... ))
 ps
ps
The sum example shows how signals represented as simple arrays can
be handled. The situation is more complex when the data layout
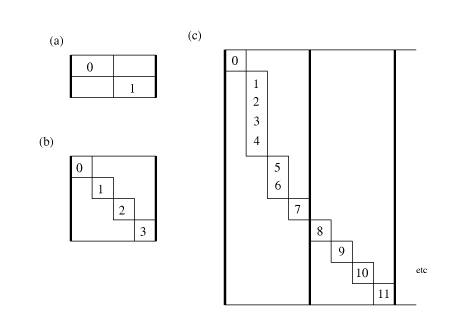
depends on dynamic values. Examples of this include sparse matrix
representations, run-length encoded vectors (Figure combined(c)) , and strings with escape sequences. Figure escape shows how 15-bit values might be encoded into an 8-bit stream
while keeping the shift offsets static. It works because both sides
of the conditional of v are specialized.
Read_esc is a good example of the failure of the
dynamic-conditional heuristic. Unless we mark the recursive call as
dynamic (so instead of inlining, the memo-table is checked),
specialization would diverge because some strings are never aligned,
as illustrated in Figure nonterm.
fun read_esc from to r =
if from = to then r
else let val v = load_sample from 8
in if v < 128 then
read_esc (from + 8) to (v + r)
else dcall read_esc (from + 16) to
((((v & 127) << 8) |
(load_sample (from + 8) 8)) + r)
end
dcall.
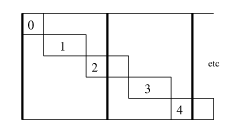 ps
psdcall annotation in read_esc.The remaining inefficiency of the code in Figure resid1 stems from the repeated loads. The standard approach to eliminating them is to apply common subexpression elimination (CSE) and aliasing analysis (see Section 10.8 of [ASeUl86]) to residual programs. Efficient handling of stores is beyond such traditional techniques, however. We propose fast, optimistic sharing and static caching as an alternative.
We implement this by replacing the load_word primitive with a
cached load procedure load_word_c. The last several addresses and
memory values are stored in a table; when load_word_c is called
the table is checked. If a matching address is found, the previously
loaded value is returned, otherwise memory is referenced, a new table
entry is created, and the least recently used table entry is
discarded. Part of the implementation appears in Appendix cache. In fact, any cache strategy could be used as
long as it does not depend on the values themselves.
The cache could be held in a global variable if the specializer supports them. We chose to transparently thread an additional argument through all calls and returns by changing its implementation language.
Note that safely eliminating loads in the presence of stores requires negative may-alias information (knowing that values will not be equal) [Deutsch94]. We have not yet implemented anything to guarantee this.
A conspicuous variable is the size of the cache. How many previous
loads should be remembered? Though this is currently left to the
programmer (with init-cache in Nitrous), automation appears
feasible. In Nitrous, if the cache is too small then some redundant
memory operations will remain; if the cache is too large then
excessive and redundant residual code is emitted. In the Simple
implementation, there are no dynamic conditionals inside of loops, so
this is not an issue.
How does the cache work? Since the addresses are dynamic, the equality test of the addresses used to determine cache membership will be dynamic. Yet these tests must be static to eliminate the cache. Our solution is to use a conservative early equality operator for the cache-hit tests; it appears in Figure earlyequal.
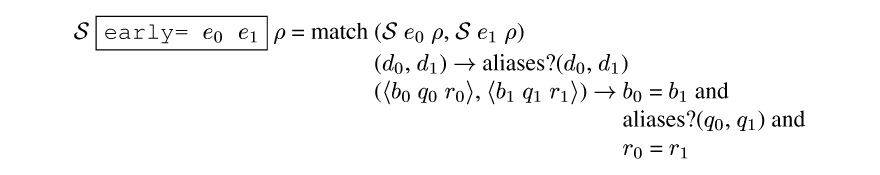
early=.This operator takes two dynamic values and returns a static value. The result is true only if the compiler can prove the values will be equal by using positive alias (aka sharing) information. The aliasing information becomes part of the static information given to compilers, stored in the memo tables, etc. For example, a procedure with three dynamic arguments can have five different versions (all equal, none equal, and three ways of two being equal).
In the Nitrous implementation the generated compilers keep track of
the names of the dynamic values. The aliases? primitive merely
tests these names for equality. Thus at compile time a cached load
operation requires only a set-membership operation. These names are
also used for inlining without a postpass (among other things), so no
additional work is required to support early=. More explanation
appears in Section mycogen.
The cache functions like a CSE routine that examines only loads, so we expect a cache-based compiler to run faster than a CSE-based one. But since CSE subsumes the use of a cache and is probably essential to good performance anyway, why do we consider the cache? Because CSE cannot handle stores, but the cache does, as explained below.
Like the optimizations of the previous section, these load optimizations have been achieved by making the compiler generator more powerful. Even more so than the previous section, the source program had to be written to take advantage of this. Fortunately, with the possible exception of cache size, the modifications can be hidden behind ordinary abstraction barriers.
Now let us see the implication of sharing to the addition rule we
defined in Figure addmult0. This addition rule contains a
dynamic addition to the quotient. In many cases ![]() is zero so the
addition may be removed by the backend. The Simple system works this
way. There is a further problem, however: a dynamic addition causes
the allocation of a new location, thus losing equality/sharing
information (Figure lesi). The multiplication rule has its
own defect: in order to maintain normal form we must dissallow
negative scales.
is zero so the
addition may be removed by the backend. The Simple system works this
way. There is a further problem, however: a dynamic addition causes
the allocation of a new location, thus losing equality/sharing
information (Figure lesi). The multiplication rule has its
own defect: in order to maintain normal form we must dissallow
negative scales.

let val y = (set-base y 4)
val x = y
val yy = y + 4
val xx = x + 4
in (early= xx yy)
end
The rules used by Nitrous appear in Figure addmult1. They are
simpler and more general because they do not maintain normal form
(recall that a cyclic value ![]() is in normal form if
is in normal form if
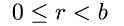 ). Without further adjustment, use of the new
addition rule would result in frequent non-termination because there
is no case that emits dynamic additions. To compensate, cyclic values
are returned to normal form at memo points: I call this late
normalization of cyclic values. The extra information propagated by
this technique (early-equality through fixed points) is required to
handle multiple overlapping streams of data.
). Without further adjustment, use of the new
addition rule would result in frequent non-termination because there
is no case that emits dynamic additions. To compensate, cyclic values
are returned to normal form at memo points: I call this late
normalization of cyclic values. The extra information propagated by
this technique (early-equality through fixed points) is required to
handle multiple overlapping streams of data.
Nitrous implements this as follows. When a compiler begins to make a dynamic code block, all cyclic values are normalized by adjusting r and emitting counter-acting additions to q. The sharing between these values must be maintained across this adjustment. Identifying all cyclic values is difficult because they may be hidden in the stack or closures, see Section ss.
So far we have only considered reading from memory, not writing to it. Storing samples is more complicated than loading for two reasons: an isolated store requires a load as well as a store, and optimizing stores most naturally requires information to move backwards in time. This is because if we read several words from the same location, then the reads after the first are redundant. But if we store several words to the same location, all writes before the last write are redundant.
We can implement store_word_c the same way a hardware write-back
cache does ([HePa90] page 379 in the second edition): cache lines
are extended with a dirty flag; stores only go to memory when a cache
line is discarded. The time problem above is solved by buffering the
writes.
The load is unnecessary if subsequent stores eventually overwrite the entire word. I achieved this by extending the functionality of the cache to include not just dirty lines, but partially dirty lines (this is sometimes called sectoring) Thus the status of a line may be either clean or a mask indicating which bits are dirty and which are not present in the cache at all. When a clean line is flushed no action is required. If the line is dirty and the mask is zero, then the word is simply stored. Otherwise a word is fetched from memory, bit-anded with the mask, bit-ored with the line contents, and written to memory. Note that the masks in the cache lines imply that the implementation substrate support native-sized integers.
Here is an example. Figure ramp shows code that stores an
increasing series of integers into every sample of a signal. Figure
ramp0088 shows the result of specializing it to a case where
loads are unnecessary. Figure ramp00816 shows the result when
the stores are non-continuous, resulting in a different expansion of
the flush_line procedure (see Appendix cache). In these
figures, the delaying effect of the cache on writes has been removed
to make the code clearer. Actual residual code from Nitrous for the
continuous case appears in Figure ramp0088r. Note how the
dynamic part of cache appears as arguments to procedures, and the
duplication of the procedure into entry and steady-state
(write-pending) versions.
fun ramp (from, to, size, stride, i) = if from = to then () else (store_sample(from, size, i); ramp (from+stride, to, size, stride, i+1))
fun ramp_0088 (from, to, i) =
if from = to then () else
let i1 = i+1 i2 = i1+1
i3 = i2+1 i4 = i3+1
(store_word(from, i | i1<<8 | i2<<16 | i3<<24);
ramp_0088 (from+1, to, i4))
fun ramp_00816 (from, to, i) =
if from = to then () else
let i1 = i+1 i2 = i1+1
(store_word(from, ((load_word from) & 0xff00ff00)
| i | i1<<16);
ramp_00816 (from+1, to, i2))
ramp_0088(k from to i) {
if (from = to) (car k)()
let i1 = i+1 i2 = i1+1
i3 = i2+1 i4 = i3+1
ramp2(k from+1 to i4 from
(i<<0 | i1<<8 | i2<<16 | i3<<24))
}
ramp2(k from to i a v) {
if (from = to) (store_word(a, v);
(car k)())
let i1 = i+1 i2 = i1+1
i3 = i2+1 i4 = i3+1
store_word(a, v);
ramp2(k from+1 to i4 from
(i<<0 | i1<<8 | i2<<16 | i3<<24))
}
root showing threading of
dynamic part of cache. The cache is held in the variables a and
v. The notation is the intermediate language described in Section
il.
This section discusses (but does not prove) the correctness of ![]() and of bit-addressing. In the introduction, I claimed that
specialization ``preserves the semantics'' of programs. Thus the
standard measure of correctness of specializers is satisfaction of the
first Futamura projection:
and of bit-addressing. In the introduction, I claimed that
specialization ``preserves the semantics'' of programs. Thus the
standard measure of correctness of specializers is satisfaction of the
first Futamura projection:
Note that this is a strong notion of correctness, defined by
equivalence of terms. [GoJo91] contains such a proof for
![]() -mix where the equivalence permits
-mix where the equivalence permits ![]() -conversion
(renaming variables). A similar proof for
-conversion
(renaming variables). A similar proof for ![]() would be
unremarkable, except for the handling of the extension for cyclic
integers. Here, the proof would use algebraic properites of the rules
in Figures addmult0 and morerules. Because
would be
unremarkable, except for the handling of the extension for cyclic
integers. Here, the proof would use algebraic properites of the rules
in Figures addmult0 and morerules. Because ![]() 's
rules for division and remainder may report errors, and because
's
rules for division and remainder may report errors, and because ![]() may not terminate, we can only prove partial equivalence, that
is, if both sides of the equation are defined, then they are
equivalent (up to
may not terminate, we can only prove partial equivalence, that
is, if both sides of the equation are defined, then they are
equivalent (up to ![]() -conversion). Note that the correctness
of polyvariant specialization and memoization has so far remained
unaddressed.
-conversion). Note that the correctness
of polyvariant specialization and memoization has so far remained
unaddressed.
Safe handling of side-effects requires maintaining the order of
computations. I believe the standard solution of let-insertion [BoDa91] could be incorporated to ![]() without problems. Nitrous
preserves order of computation because it processes programs in
continuation-passing style.
without problems. Nitrous
preserves order of computation because it processes programs in
continuation-passing style.
However, treating memory operations as generic side-effects is too
restrictive (an exception is when the memory is mapped to an I/O
device). Show that bit-addressing is correct requires proving that
the cache preserves the ordinary semantics of a memory system[footnote: The ordinary semantics of memory guarantee that reading location ![]() returns the last value written to location
returns the last value written to location ![]() .]. Proofs of this
kind are standard and, with one exception, I see no problem developing
one for a software cache.
.]. Proofs of this
kind are standard and, with one exception, I see no problem developing
one for a software cache.
The problem stems from the conservative early equality. Correctness depends either on finding some way to guarantee negative may-alias information, or a relaxed definition of correctness. One way to make the guarantee is to dynamically verify pointer inequality (for example, before entering a loop). If the data layout is irregular then maintaining the guarantee is very difficult. Until an inexpensive way to make guarantees is found, I choose to live dangerously.
Correctness of sharing is part of the satisfaction of the Futamura projection given above.
Late normalization is more interesting. Showing that the modified rules of Figure addmult1 are algebraically correct is not hard. The danger of late normalization is non-termination, so a proof of partial equality is not revealing. The useful proof is that late normalization does not introduce non-termination.
Specialization, as described in Chapter pe and extended in Chapter bit-addr, is unable to perform many useful optimizations. This section give some examples and suggests how to achieve them.
f : a -> c g : c -> b l : a list map : (a -> b) -> a list -> b listmap f (map g l) --> map (f o g) l
o, as
usual.An important transformation on programs that process streams of data is loop fusion. In the functional language community, a general form of this optimization is known as deforestation [Wadler88]. This transformation eliminates intermediate data structures, as illustrated in Figure dforest. Furthermore, optimizing compilers for numerical and data-parallel languages such as High Performance Fortran and NESL perform extensive analysis to determine how to divide the computation into passes, layout the data-structures in memory, and coordinate multiple processors [SSOG93, ChaBleFi91].
Partial evaluation alone does not solve these problems. Specializing
map f (map g l) has no effect. Instead, my approach is to specify
procedures directly in one pass, and use specialization to efficiently
implement (f o g). Similarly, I believe specialization could be
effective as a middle stage in such a compiler.
Another important kind of code one would like to remove is clipping
and array-bounds checks. For example, frequently one can guarantee
that some raster operations will be unobscured and in-bounds, and thus
avoid clipping operations. The natural way to handle this with a
specializer is to propagate additional static information. For
example, one might statically know that 10 < i < 100. As usual,
this can be done by manual binding-time improvement or by improving
the specializer. The latter route leads to the technique of generalized partial computation [FuNoTa91, SoGluJo96],
wherein PE is extended with a theorem prover.
Say we wrote bitcopy in bit-serial fashion, as in Figure bsbc. The rules of this chapter produce (assuming an 8-bit word for brevity) the obviously inefficient code in Figure bc8.
fun bitcopy (start, stop, start0) = if start=stop then () (store_sample(start0, 1, load_sample(start, 1)); bitcopy(start+1, stop, start0+1))
fun bitcopy_000(start, stop, start0) =
if start=stop then ()
let v = load_word(start)
store_word(start0, (v&1) | (((v>>1)&1)<<1)
(((v>>2)&1)<<2) | (((v>>3)&1)<<3) |
(((v>>4)&1)<<4) | (((v>>5)&1)<<5) |
(((v>>6)&1)<<6) | (((v>>7)&1)<<7));
bitcopy_000(start+1, stop, start0+1)
The problem is that the source program uses a single bit of the input stream as an intermediate value. The bits are then just reassembled into words. There appear to be two parts to the problem: tracking where individual bits of data go, and then when a word is finally really needed, determining how to assemble that bit-pattern with available hardware (in the above case, it would determine that no work at all is needed).
We now speculate on how to provide this optimization with a specializer. Introduce a new binding time, that is another kind of partially static integer: masked. The static part includes a mask indicating which bits are known, what those bits are, and source information for each dynamic bit. Operations such as shifting and masking can then be performed statically, simply by rearranging the dynamic bits. When one of these values is passed to an unknown primitive, it is lifted to a simple value, and the assembly routine is invoked.
This chapter added cyclic integers to the specializer from the last chapter. Use of these partially static integers combined with the memoization results in smart loop unrolling. In order to optimize memory operations with stores, we implement a cache in software. The cache is controlled by aliasing information in the compiler. Together, these allow us to write signal processors independent of the signal's representation (at least, relativly independent when compared to other languages). The results of building some software with this kind of interface appears in Chapter benchmarks. The next chapter (Chapter system) explains how the Nitrous implementation works in detail.