Nitrous[footnote: It is named for nitrous oxide ![]() , a gas used
to make cars go really fast. It is also a common medical anaesthetic.
William James found that its subjective effect was to reveal the
Hegelian synthesis [James1882].] is a compiler generation system.
It accepts a program in a full-featured source language and transforms
the program into a compiler. Because it runs very slowly and the
constant propagation is aggressive, excessively large compilers and
residual code is a problem. The objective of the design was to
demonstrate that enough static information is available to make
transformations like those of Section application and Chapter
bit-addr work. For example, one might wonder if higher-order
functions or safety conflicts with late normalization of partially
static integers or early equality.
, a gas used
to make cars go really fast. It is also a common medical anaesthetic.
William James found that its subjective effect was to reveal the
Hegelian synthesis [James1882].] is a compiler generation system.
It accepts a program in a full-featured source language and transforms
the program into a compiler. Because it runs very slowly and the
constant propagation is aggressive, excessively large compilers and
residual code is a problem. The objective of the design was to
demonstrate that enough static information is available to make
transformations like those of Section application and Chapter
bit-addr work. For example, one might wonder if higher-order
functions or safety conflicts with late normalization of partially
static integers or early equality.
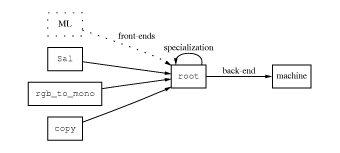
Root is the intermediate language at the center of the system, it
is described below. Figure system-block identifies the three
kinds of program transformations within Nitrous:
root programs from programs in
user-defined languages. Though the front-ends discussed here are
all automatically generated by the system, the design is meant to
support hand-written front-ends, such as an ordinary ML compiler.
root.
The specializer is a compiler generator cogen. This chapter
explains the mechanics of how cogen works, including the
intermediate language and some important front-ends.
 ps
ps
Root is a simple abstract machine code, like higher-order
three-address-code ([ASeUl86], p. 466) with an unlimited number
of registers and in continuation-passing closure-passing style
(CPS-CPS) [Appel92]. Thus the stack in a root program is
explicitly represented as a data structure. The model includes data
structures, arithmetic, an open set of primitive functions, and
represents higher-order values with closures.
A language supports reflection if it can convert a data structure
representing an arbitrary program text into a value (possibly a
function). Lisp supports reflection with eval and compile.
Reification is the opposite of reflection, that is, converting a
value (possibly a function) into a corresponding text. Although
reification is commonly available in debuggers and interpreters, not
even Common LISP standardizes it. [FriWa84] defines and
discusses these ideas in detail. Reification is sometimes called
introspection [Thiemann96] Section 4.
Root supports both reflection and reification. By supporting
reflection we make code-producing functions first class. Nitrous
takes this a step further by using reification to make the
compiler-producing function first class: rather than working with
files, cogen just maps procedures to procedures.
Sal is a recursive-equations language augmented with lambda
and various convenience features. The cogen-created compiler
produces straight-forward code. It performs CPS-CPS conversion and
compiles tail-recursive calls without building stack frames, but is
otherwise non-optimizing. Sal is covered in Section sal.
Rgb_to_mono (from Figure rgbm) and copy (from Figure
sig) are two example media processing languages. The
interpreters for these languages were written in Sal.
Nitrous implements specialization in two stages: cogen transforms
a root program and binding times (BTs) for its arguments into a
generating extension. The extension is executed with the static
values to produce the specialized residual program. The BTs
categorize each argument as static program or dynamic data. The
extension consists of a memo table, followed by the static parts of
the computation interleaved with instructions that generate residual
code (i.e. do RTCG).
Because the compilers produce the same language that cogen accepts,
and the root text of the residual programs is easily accessible,
multiple layers of interpretation can be removed by multiply applying
cogen. For example the output of the Sal compiler is valid input to
cogen. This is how rgb_to_mono and copy were built. The
lift compiler (see Section structlift) also uses two layers.
Another possibility is to include a compiler generator as a primitive
in Sal.
Multi-stage application requires that the generated compilers create correctly annotated programs, which can be difficult. In [GluJo94, GluJo95] Glück and Jørgensen present more rigourous and automatic treatments of layered systems using specializer projections and multi-stage binding-time analysis.
This chapter is organized as follows. First, the intermediate language is presented, followed by the compiler generator, the Sal front end, and the conclusion. The bulk of the material consists of technical details of the compiler generator.
The core of the system is the intermediate language. Its formal
syntax appears in Figure root-syntax. A program is called a
code pointer, or just a code. When a code is invoked, its formal
parameter list is bound to the actual arguments. The list of prim
and const instructions execute sequentially, each binding a new
variable. If tests a variable and follows one of two instruction
lists. These lists terminate with a jump or exit instruction.
A jump invokes the code bound to the first argument. The
remaining arguments form the parameter list, and the cycle repeats
itself. Exit stops the machine and returns an answer. Formal
semantics appear in Figure root-semantics. The semantics are
given in Scheme [R4RS], extended with a pattern-matching macro.

Root syntax. As usual, * and + superscripts denote lists of
length zero-or-more and one-or-more, respectively.
(define (eval-root code args)
(match code
(('code name formal-args source-code)
(let loop ((instrs source-code)
(env (zip formal-args args)))
(let ((lu (lookup env)))
(match instrs ; not just the car
((('exit arg)) (lu arg))
((('jump fn . args))
(eval-root (lu fn) (map lu args)))
((('if pred t-branch) . f-branch)
(if (lu pred)
(loop t-branch env)
(loop f-branch env)))
((('const var c) . rest)
(loop rest (cons (cons var c) env)))
((('prim var prim . args) . rest)
(let ((v (apply prim (map lu args))))
(loop rest (cons (cons var v) env))))))))))
root in Scheme.Structured higher-order control flow is managed with closure-passing [Appel92]. A closure is a pair consisting of a code pointer with its bound variables, and is invoked by jumping to its left member and passing itself as the first argument. A normal procedure call passes the stack as the next argument. The stack is just the continuation, which is represented with a closure.
See Figure append-eg for an example program in root that
uses a stack. Notes: a return by jumping to the car of k,
passing k and m as arguments. b These constants are
codes not symbols (append is a circular reference). c close is like cons, but identifies a closure. Figure app2-eg shows the same program in the abbreviated syntax used in the
remaining examples. d destructuring assignment expands into
car/cdr chain. Figure aper shows how to evaluate this
program. Figure ho-eg shows a higher-order program.
(code append (k l m)
((prim t0 null? l)
(if t0 ((prim t1 car k)
(jump t1 k m))) ; a
(prim frame list k l m)
(const cont cont) ; b
(prim cl close cont frame) ; c
(prim t2 cdr l)
(const append append) ; b
(jump append cl t2 m)))
(code cont (self r)
((prim t0 cdr self)
(prim k car self)
(prim t1 cdr t0)
(prim l car t1)
(prim t2 cdr t1)
(prim m car t2)
(prim t3 car l)
(prim nr cons t3 r)
(prim t4 car k)
(jump k nr)))
Root code for append, in literal syntax. See text
for notes.
append(k l m) {
if (null? l) (car k)(k m) ; a
frame = (list k l m)
cl = (close cont frame) ; b c
append(cl (cdr l) m) ; b
}
cont(self r) {
(k l m) = (cdr self) ; d
nr = (cons (car l) r)
(car k)(k nr)
}Root code for append, in sugary syntax. See text for notes.
compose(k f g) {
lam = (close apply_g (list f g))
(car k)(k lam)
}
apply_g(k self x) {
(f g) = (cdr self)
cl = (close cont (list k f g))
(car g)(g cl x)
}
cont(self r) {
(k f g) = (cdr self)
(car f)(f k r)
}Root code for compose, showing how closures and higher-order
calls work.
(define top-cont '((code top-cont (self r) ((exit r)))))(eval-root append-root (list top-cont '(1 2 3) '(4 5)))
-->
(1 2 3 4 5)
append (which is bound to the Scheme variable append-root to
avoid conflict with the native version). Top-cont is a stub
continuation that returns a value to the Scheme metalevel.
Factors that weigh in favor of an intermediate language like root
instead of a user-level language like Scheme or SML: it makes cogen
smaller and easier to write; it provides a target for a range of
source languages; it provides an interface for portability; it exposes
language mechanism (such as complex optional arguments, pattern
matching, method lookup, or multi-dimensional arrays) to partial
evaluation; it reduces assembly overhead because it is essentially an
abstract RISC code.
Two factors that weigh against root: explicit types would simplify
the implementation and formalization, and on some architectures good
loops (e.g. PC-relative addressing or other special instructions) are
difficult to produce. Using a language like the JVM [GoJoSte96],
or one of the intermediate languages of [TMCSHL96] would leverage
existing research.
Cogen is directly implemented (rather than produced by
self-application), polyvariant in binding times (it allows multiple
binding time patterns per source procedure), performs polyvariant
specialization with memo-tables, and handles higher-order control
flow. This section summarizes how cogen and its extensions work.
The subsections cover the implementation of binding times, cyclic
integers, lifting, static extensions, special primitive functions,
shape un/lifting, and dynamic control stacks.
While Nitrous does very well with small examples, several flaws make scaling difficult. Nitrous is apt to classify too much computation as static and produce large amounts of residual code, thus requiring the programmer to make careful use of lifting. Several expediencies made its developement easier, but increased the code output. Section simple describes an implementation that scales better by using a restricted language.
One interesting feature of Nitrous is that the input language is in continuation-passing style. This has three results: let-insertion for safety is avoided, dynamic choice of static values is supported, and the generated compilers do CPS transformation.
Although the input language is not explicitly typed, it turns out that annotations marking particular values as stacks and closures are essential. This indicates that an explicitly typed input language would work better.
Cogen converts a code and a binding-time pattern to a metastatic extension. A metastatic extension is denoted with the
name of the code pointer and the BT pattern, for example append(. The extension takes the static values and the names of the
dynamic values and returns a procedure---the specialized code. Figure
apsh shows an example session.
D
S D)
(define append-DSD (cogen append-root
'(dynamic static dynamic)))
(eval-root append-DSD
`(,top-cont
(1 2 3)
,(var->shape 'k)
,(var->shape 'm)))
-->
append-123(k m) {
(car k)(k (cons 1 (cons 2 (cons 3 m))))
}
Inlining is controlled by the dynamic conditional heuristic (see
Section practical), but setting the special $inline
variable overrides the heuristic at the next jump (see Figures fdts and do-call for examples).
In CPS-CPS continuations appear as arguments, so static contexts are
naturally propagated. Figure dyn-if shows the translation of
(+ s (if d 2 3)) into root and the result of specialization.
This is the effect refered to in Section features.

Binding times are properties derived from the interpreter text while a
compiler generator runs. In the formal system of Chapter pe,
they were the injection tags on values in ![]() . Primarily they
indicate if a value will be known at compile time or at run-time, but
they are often combined with the results of type inference, control
flow analysis, or other static analyses. Binding times are sometimes
called metastatic values because in self-application of a
specializer, they are static at the meta-level (the outer
application).
. Primarily they
indicate if a value will be known at compile time or at run-time, but
they are often combined with the results of type inference, control
flow analysis, or other static analyses. Binding times are sometimes
called metastatic values because in self-application of a
specializer, they are static at the meta-level (the outer
application).
Cogen's binding times are described by the grammar in Figure
lo. The binding times form a lattice where ![]() and
and ![]() . Thus
. Thus D is the bottom
of the lattice, though this contradicts the metaphore suggested by
``lifting''. Circular binding-times are allowed, so binding-times may
have infinite size as long as they are recognized by a context-free
grammar. The join operation of the lattice is not used by Nitrous,
but the following equations define it for finite binding-times:

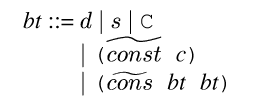 S
-> C -> D; S -> cons -> D; }}">
S
-> C -> D; S -> cons -> D; }}">D denotes
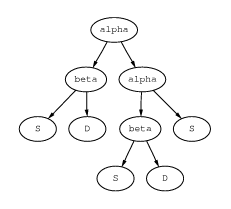
dynamic, S denotes static, C denotes cyclic, and Cons cells are handled by representing binding times with graph-grammars as Mogensen did. Pairs in binding times are labeled with a cons point that identifies which instruction the pair came from. If the same label appears on a pair and a descendant of that pair then the graph-grammar is collapsed, perhaps forming a circularity [Mogensen89]. Figures collapse and colla2 show two possibilities.
The function of the cons-points would be better provided by explicit inductive types.
 ps
ps
 ps
psalpha appears twice and the graph
is collapsed, forming a circularity.
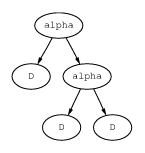 ps
ps 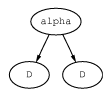 ps
ps alpha appears twice and the
graph is collapsed, not forming a circularity.
We denote such a pair ![]() (the
label is invisible here).
(the
label is invisible here). ![]() abbreviates
abbreviates ![]() . We use familiar type constructors to denote
circular binding times. Figure bt-eg depicts several useful
examples.
. We use familiar type constructors to denote
circular binding times. Figure bt-eg depicts several useful
examples.
As in Schism [Consel90], control-flow information appears in the
binding times. Cogen supports arbitrary values in the binding
times, including code pointers, the empty list, and other type tags.
Such a binding time is denoted ![]() , or
just c.
, or
just c.
Closures are differentiated from ordinary pairs in the root text,
and this distinction is maintained with a bit in ![]() binding
times. Such a binding time is denoted
binding
times. Such a binding time is denoted ![]() .
.
An additional bit on pair binding times supports a sum-type with
atoms. In terms of a grammar, a ![]() with this bit set may be
either a pair or an atom (a terminal). The bit is set during collapse
if a cons is summed with an atom; in Figure collapse the bit
is set on
with this bit set may be
either a pair or an atom (a terminal). The bit is set during collapse
if a cons is summed with an atom; in Figure collapse the bit
is set on alpha. In Figure colla2, the bit is not set.
The bit is not denoted.
 ps
ps  ps
ps  ps
ps(S * D) list is typically used
as an association list
from static keys to dynamic values, D list is a list only whose
length is static, stack-bt is the binding time of a control
stack.
Nitrous can break an integer into static base, dynamic quotient, and
static remainder, as described in Section cyclic. In the
lattice, S<C<D. We have to make special cases of all
the primitives that handle cyclic values; these were introduced in
Section cyclic. See Section prims for a description
of the other special primitives.
Extensions rename the variables in the residual code and keep track of the shapes (names and cons structure) of the dynamic values. The shape of a simple dynamic value is the name of the variable that will hold the value. If the shape of a value is a pair of names, then the dynamic value is held in two variables. Shapes always mirror the binding times. In partial evaluation jargon, the effect of using shapes is called variable splitting or arity raising.
In Figure apsh, the binding time of the third argument is D,
so its shape must be just a name. In Figure apsh2, the
binding time is D list, so the shape is a list of names. In
Figure apsh3 the binding time is the same, but because Nitrous
uses the sharing information from the identical names in the
shape, only two values are passed instead of four.
Shapes are part of the key in the static memo-table. Two shapes match only if they have the same aliasing pattern, that is, not only do the structures have to be the same, but the sharing between parts of the structures must be the same. This can be computed in nearly-linear time.
The effect of variable splitting is that the members of a structure
can be kept in several registers, instead of allocated on the heap
(abstracted into one register). The effect of sharing is that if two
of the members are known to be the same, they only occupy one
register. This comes down to adding equational constraints to the
static information. This is why the residual code from rgb_to_mono in Figure rgbm1 has fewer arguments than Figure
rgbm2.
(define append-DSD* (cogen append-root `(dynamic static ,(make-list-bt 'dynamic))))(eval-root append-DSD* `(,top-cont (2 3) ,(var->shape 'k) ,(map var->shape '(a b c)))) --> append-23abc(k a b c) { t = (cons a (cons b (cons c '()))) (car k)(k (cons 2 (cons 3 t))) }
Make-list-bt creates D list from D.
(eval-root append-DSD*
`(,top-cont
(2 3)
,(var->shape 'k)
,(map var->shape '(a b b a))))
-->
append-23abba(k a b) {
t = (cons a (cons b (cons b (cons a '()))))
(car k)(k (cons 2 (cons 3 t)))
}Lifting is generalization, or abstracting away information. If we abstract away the right information the compiler will find a match in its memo table, thus proving an inductive theorem and forming a dynamic loop. The simplest lift converts a known value to an unknown value in a known location (virtual machine register). Lifting occurs when
code is converted to a static value.
prim has arguments of mixed binding time, causing all the
arguments to be lifted.
jump has dynamic target, causing all the arguments to be
lifted.
Lifting is inductively defined on the binding times. The base cases are:
set-base.
cons instruction.
p((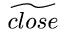
D x) D D ...) (all but the first
argument are D), then emits the cons pairing the specialized code
with the dynamic values.
Cases 5 and 6 are particularly interesting. Any static information in frame is saved by reassociating it into the code pointer before it is lifted. This introduces a complication, as explained in Section unlift below.
Manual lifting is supported in root with an instruction understood
by cogen but ignored by the root semantics:
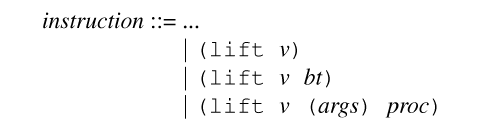 The variable v is lifted to
The variable v is lifted to D, unless the target bt is
given. Any legal lift is supported, including lifting to/from
partially static structures with loops and closures. Instead of
giving a binding time bt, one can give a procedure proc
which is executed on the binding times of args. This provides a
gateway to Scheme for the lift language.
A delayed lift, denoted ![]() , produces a
residual lift at time
, produces a
residual lift at time ![]() . If
. If ![]() is zero, then it functions as
an ordinary lift defined above.
is zero, then it functions as
an ordinary lift defined above.
If a lift is not one of the base cases outlined above, then the lift compiler is invoked to create a procedure that takes the value
apart, applies simple lifts at the leaves, and reassembles the
structure. Cogen inserts a call to this procedure into the source
program, and recurses into it.
For example, consider the lift ![]() . The compiler has a list of values and a list of
variable names. It recurses down the lists, and emits a const and a
cons instruction (making a binding) for each list member. At the base
it recovers the terminator, then it returns up and emits cons
instructions that build the spine. The copy function appears in
Figure lce, and its specialization in Figure lcer.
. The compiler has a list of values and a list of
variable names. It recurses down the lists, and emits a const and a
cons instruction (making a binding) for each list member. At the base
it recovers the terminator, then it returns up and emits cons
instructions that build the spine. The copy function appears in
Figure lce, and its specialization in Figure lcer.
It turns out that this lift compiler can be created by cogen itself.
The meta-interpreter is just a structure-copy procedure that traverses
the value and the binding times in parallel. A delayed lift
annotation is used where the BTs indicate a simple lift. Specializing
this to the binding times results in a copy function with lifts at the
leaves. The value passed to the copy
function has the binding time that was just a static value. When
the continuation is finally called the remaining static information is
propagated. The copy function may contain calls to itself (where the
BT was circular) or to other extensions (to handle higher-order
values).
This is an example of multi-stage compiler generation because the
output of a generated compiler is being fed into cogen. The
implementation requires care as cogen is being used to implement
itself, but the possibility of the technique is encouraging.
(define (copy_sdl2d l)
(if (null? l)
'()
(let ((hd (car l))
(tl (cdr l)))
(cons (cons (lift (car hd))
(cdr hd))
(copy_sdl2d tl)))))
(S * D) list to D.
sdl2d1(k a b) {
(car k)(k (cons (cons a 1) (cons (cons b 2) '())))
}
Set-base is an special annotation that takes an integer with any
binding time and converts it to cyclic with a particular base. This
can be a lift, for example when going from static to cyclic base four,
or when going from cyclic base four to base two. Note that cyclic
base one is functionally the same as dynamic. Converting from dynamic
to cyclic requires case-analysis (known as The Trick in partial
evaluation jargon). Changing the base of a cyclic value may require
both of these, for example to go from base two to base three.
Lifting out a factor is easy because static information is just
discarded from the compiler. Case-analysis creates static information
by emitting dynamic conditionals and duplicating code. Nitrous
implements this by inserting a call to the procedure in Figure fdts. The argument d is the dynamic value to be converted; n
is its maximum possible value plus one; n is static. Note that
the test for the error is essential even though it may never be true,
as without it the compiler will not terminate.
finite-dynamic-to-static(k d n) {
if (zero? n) error
n1 = n - 1
if (n1 = d) $inline = #t
(car k)(k n1)
$inline = #t
finite-dynamic-to-static(k d n1)
}
Cogen treats some primitive functions specially, generally in
order to preserve partially static information. Figure special-ops gives the improved binding times possible, and in what
situations they occur. Notes:
root is untyped.
Null? and atom? are also supported.
apply takes two arguments: a primitive (in one
back-end a C function, in the other a Scheme procedure) and a list
of arguments. If the primitive and the number of arguments are
static, then the compiler can just generate the primitive instead
of building an argument list and generating an apply. This
supports interpreters with an open set of primitives or a foreign
function interface. Notice this does not improve the binding
times, it just generates better code.
S and D are created, the
compiler chooses one statically (see Section cyclic).
early= conservative static equality of dynamic
values, see Section loads.
(identity x) x a (cons S S) Sb (cons S D) 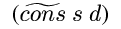
(cons D D) 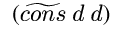
c (car  )
) x (pair?  )
) Sd (apply S (D list)) De (+ C S) C(* C S) C(+ D S) C(* D S) C(zero? C) S Df (imod C S) S(idiv C S) C(early= D D) Sg
Previously [Draves96], the code pointer in a static closure (from a function or a continuation) was represented with a metastatic extension. The binding times in such an extension are fixed, which restricted the use of polyvariance and required additional annotation. Specifically, when you made a static stack frame you had to give the binding time of the return value. This conflicts with the polyvariance in the binding times needed to support bit-addressing.
Furthermore, the implementation of late normalization of cyclic values (Section npi) requires being able to identify all cyclic values in the static state of the compiler.
I solved these together by changing the representation of extension to include the original code pointer and the binding time of the first argument (i.e. the frame inside the closure). So when the compiler is running and the static extension is called, the rest of the binding times are available. At this point we call cogen to get the metastatic extension, and then jump to that. Because we memoize on binding times, this results in lazy compiler generation; cogen is called at compile time. In this way, Nitrous is a hybrid between offline and online systems like [Sperber96].
This was a big change conceptually, but a small change in terms of the code and what actually happens.
There are two places where static extensions are created: static recursions and higher-order values.
Because the stack is an explicit argument, when cogen encounters a
static recursion the same label will eventually appear on two stack
frames. In theory, because ![]() , when this loop is collapsed the metastatic
continuations would be lifted to static, thereby converted to
extensions and forming a control stack in the compiler[footnote: If
instead of forgetting x and y completely, we approximated
them with a set, the result would be control-flow analysis based on
abstract interpretation [Shivers91].]. However, to simplify the
implementation
, when this loop is collapsed the metastatic
continuations would be lifted to static, thereby converted to
extensions and forming a control stack in the compiler[footnote: If
instead of forgetting x and y completely, we approximated
them with a set, the result would be control-flow analysis based on
abstract interpretation [Shivers91].]. However, to simplify the
implementation cogen uses a special lift that makes a static
extension:
![]() This saves v and its binding time in a static extension, and
sets its binding time to stack-bt.
This saves v and its binding time in a static extension, and
sets its binding time to stack-bt.
For example, consider specialization of append[footnote: Only a
irregular recursion really requires this, but append is easier to
understand.]. The source with annotations appears in Figure stack-lift. When cogen is called to create append(, it calls itself recursively to create D S
D)append(stack-bt S
D), causing a recursive call to create append(stack-bt S D)
again. Since this binding-time pattern is now in the memo-table, the
recursion terminates. There are two extensions made from append.
The difference is the jump to the continuation in the base case. In
the first the jump target is dynamic, in the second it is static (but
not constant). If the list is not zero length then when we call append(stack-bt S D) with the static values, then each time the
compiler returns it is a call to a static extension. The first return
creates cont((.
Subsequent returns except for the last one request the same
binding-time pattern, which is in the memo-table. Figure slt
illustrates this series of events. Note that there are two versions
of each extension. ![]() cont (
cont (![]() stack-bt S D)) D)
stack-bt S D)) D)Cogen could avoid producing the (probably
over-) specialized entry/exit code by checking for the end of the
stack explicitly. Static extensions are also created for source
lambda abstractions, see the case lambda? in Appendix sal-src.
Late normalization of cyclic values requires that all cyclic values be identified and simultaneously normalized at the beginning of the construction of a dynamic code block (after checking the memotable). These values are identified by their binding times. So we need the binding times of the values inside of closures and the stack. This is the other reason.
append(k l m) {
if (null? l) (car k)(k m)
frame = (list k l m)
cl = (close cont frame)
lift cl stack
append(cl (cdr l) m)
}
cont(self r) {
(k l m) = (cdr self)
nr = (cons (car l) r)
lift nr
(car k)(k nr)
}
append(D S D)
append(stack-bt S D)
*append(stack-bt S D)
cont(( cont (
cont ( stack-bt S D)) D)
*cont((
stack-bt S D)) D)
*cont(( cont (
cont ( stack-bt S D)) D)
*cont((
stack-bt S D)) D)
*cont(( cont (
cont ( stack-bt S D)) D)
...
cont((
stack-bt S D)) D)
...
cont(( cont (
cont ( D S D)) D)
D S D)) D)
* indicates
a hit on the memo-table.
Here we consider lift case 5 from Section lifting in greater
detail. Say f has one argument besides itself. Then lifting
![]() creates a call
to the extension
creates a call
to the extension ![]() .
The extension is used to fold the static part of frame into
.
The extension is used to fold the static part of frame into f. The problem is, according to its binding-time pattern, the
extension expects the dynamic part of the frame to be passed in
separate registers (because of variable splitting), but at the call
site the value is pure dynamic, so they are all stored in one
register.
Nitrous uses special code at the call site to save (lift) the shape, and in the extension wrapper to restore (unlift) the shape. This code optimizes the transfer by only saving each register once, even if it appears several times in the shape (typically a lexical environment appears many times, but we only need to save the subject-values once). The same optimization prevents a normal jump from passing the same register more than once.
How do we extract the dynamic stack of a Sal program from the
stack in the Sal interpreter? Say cogen encounters do-call(stack-bt (see Figure do-call). When S S alist-bt)cl is lifted we compute cont((. We want to generate a procedure
call where ![]()
S
(![]() stack-bt
stack-bt S)) D)cont jumps to apply, so inlining is disabled and we
lift the stack (k) to D, invoking lift base case 4. The problem
is the extension was made assuming the code pointer would be static,
but now it will be dynamic. The unlift code inserts an additional cdr
to skip the dynamic value, thus allowing an irregular stack pattern to
be handled.
do-call(k fn exp env) {
frame = (list k fn)
cl = (close cont frame)
lift cl stack
eval(cl exp env) a
}
cont(self arg) {
(k fn) = (cdr self)
lift k
$inline = #f
apply(k fn arg)
}
Representations of Cyclic Values
If cyclic values as described in Sections cyclic are applied to the filter example from Chapter 5, a limitation is revealed. The problem is the addresses are cyclic values so before you can load a word the address must be lifted, resulting in a dynamic multiplication and addition. One way to solve this is to use a different representation: rather than use q as the dynamic value, one can use bq. This is premultiplication. On most RISC architectures the remaining addition can be folded into the load instruction.
The disadvantage of premultiplication is that multiplication and division can no longer maintain sharing information. Which representation is best depends on how the value is used. A constraint system should suffice to pick the correct representation.
The name ``Sal'' is derived from ``sample language''. There are two
versions of Sal, one in Nitrous, and is the input to the Simple
system. This section concerns the former. After giving the syntax of
the language, this section describes its implementation with Nitrous.
Sal is basically a recursive equations language with threaded store,
let, lambda, syntactic sugar, and annotations (that is,
information ignored by the ordinary semantics of the language, but
essential to cogen). Figure sal-syntax gives a grammar for
the syntax. The semantics are obvious except as noted:
$inline variable.
See Appendix sal-src for the source code for the interpreter.
That this is root code makes it difficult to read; if written in
direct-style with high-level syntax, it would be ordinary. It could
easily be bootstrapped and implemented in Sal itself.

The compiler generated by cogen compiles Sal programs to root
programs. It works in one-pass, performing CPS conversion, closure
conversion using a linked representation, and executes
tail-recursion without the stack. It generates some duplicate code
unnecessarily, and is non-optimizing. Conversion to
continuation-passing style is a standard result in PE [Danvy96], but the others are new.
It is possible to feed this generated code back into cogen. This
is how the benchmarks of Section nitrous were done.
Examples of residual root code generated by this compiler appears
in Appendex sal-obj. They show the duplication problems, as
well as the residual annotations required for two-level
specialization.